Découvrez Comment Trouver L’aire Du Plus Grand Rectangle Inscrit Avec Des Images Explicatives. Enquête Sur La Théorie Et Les Astuces Pour Maîtriser Ce Concept.

**démonstration Géométrique : Rectangle Inscrit** Comprendre La Théorie À Travers Des Images Explicatives.

• Qu’est-ce Qu’un Rectangle Inscrit En Géométrie?
• Propriétés Fascinantes Du Rectangle Inscrit Expliqué
• Visualiser Le Concept Avec Des Images Explicatives
• Applications Pratiques Du Rectangle Inscrit Dans La Vie
• Erreurs Courantes À Éviter Dans Les Démonstrations
• Zoom Sur Des Exemples Célèbres De Rectangles Inscrits

Qu’est-ce Qu’un Rectangle Inscrit En Géométrie?

En géométrie, le concept de rectangle inscrit se réfère à un rectangle dont les sommets touchent les bords d’une forme donnée, généralement un cercle. Imaginez-vous en train de dessiner un cercle parfait ; si vous placez un rectangle à l’intérieur de ce cercle de manière à ce que chaque coin du rectangle frôle la circonférence, vous aurez alors un rectangle inscrit. Ce principe est fondamental car il crée une harmonie parfaite entre les deux figures et ouvre la voie à des propriétés mathématiques fascinantes. Comprendre ce concept enrichit véritablement notre appréciation de la géométrie et nous permet de mieux visualiser les relations entre différentes formes.

Les rectangles inscrits présentent des propriétés intéressantes qui peuvent parfois être confondues avec des calculs simples. Par exemple, les dimensions du rectangle inscrit dépendent de l’angle que fait chaque coin avec le centre du cercle. Cela signifie qu’un changement léger dans l’angle pourrait modifier l’aire du rectangle de manière significative. En mettant en lumière les analogies avec d’autres concepts mathématiques, comme la prescription (Rx) de médicaments, nous pouvons agrémenter nos explications de parallèles significatifs. En effet, tout comme la prescription doit être parfaitement adaptée au patient pour être efficace, le rectangle inscrit doit être adapté aux limites du cercle pour maximiser son aire.

Caractéristique	Description
Définition	Rectangle dont les sommets touchent un cercle.
Propriétés	Les dimensions dépendent de l’angle du cercle.
Importance	Fondamental pour l’étude des relations géométriques.

Propriétés Fascinantes Du Rectangle Inscrit Expliqué

Dans le monde fascinant de la géométrie, le rectangle inscrit présente plusieurs caractéristiques indéniables qui éveillent la curiosité de nombreux passionnés. Par exemple, lors de la conception d’un rectangle inscrit dans un cercle, sa largeur et sa hauteur peuvent varier tout en respectant des proportions spécifiques qui permettent d’optimiser l’aire. Lorsqu’on cherche à encontre a area do maior retangulo que pode ser inscrito, il devient évident que les diagonales des rectangles inscrits dans un cercle se croisent en son centre. De plus, chaque rectangle inscrit partage une propriété fondamentale : son périmètre est toujours inférieur ou égal à celui du cercle dans lequel il est inscrit, ce qui en fait un sujet idéal pour analyser des concepts d’optimisation mathématique.

Une autre facette fascinante du rectangle inscrit réside dans son application dans des scénarios concrets, comme la conception architecturale et le design graphique. Par exemple, lorsqu’un architecte conçoit un bâtiment, il a souvent recours aux principes du rectangle inscrit pour maximiser l’utilisation de l’espace tout en répondant aux besoins esthétiques et pratiques. En parallèle, ce principe peut être observé dans les médias et publicité, où les compositions visuelles respectent souvent des proportions inspirées par le rectangle inscrit. Ce lien entre théorie et pratique démontre non seulement la portée esthétique, mais également la pertinence fonctionnelle de ce concept géométrique.

Visualiser Le Concept Avec Des Images Explicatives

L’illustration du rectangle inscrit est cruciale pour bien saisir la structure géométrique sous-jacente à ce concept. En disposant un rectangle à l’intérieur d’un cercle, par exemple, on peut visualiser le lien entre les dimensions de ce rectangle et celles du cercle. Les images explicatives, qu’il s’agisse de diagrammes ou de modèles 3D, nous aident à comprendre comment la rencontre a area do maior retangulo que pode ser inscrito s’aligne avec les propriétés du cercle. Ce processus de visualisation n’est pas seulement une question d’esthétique ; il améliore aussi notre capacité à mémoriser et à évoquer des concepts complexes.

Les images jouent un rôle de catalyseur dans le processus d’apprentissage. Des schémas annotés peuvent illustrer les différentes étapes pour dessiner un rectangle inscrit, permettant ainsi de clarifier la méthode de construction et d’analyse. En regardant un schéma où les coordonnées d’un rectangle sont indiquées clairement, on peut facilement apprécier comment les angles droits et les proportions se maintiennent. Chaque image évoque des exemples réels, et visualiser ces concepts dans différentes configurations aide à solidifier notre compréhension. Cela permet également d’éviter des erreurs communes, en mettant en lumière des détails souvent négligés.

Plusieurs applications se présentent alors même que nous cherchons à imager ce concept. Imaginez une situation dans une pharmacie, par exemple, où un pharmacien doit établir un espace optimal pour accueillir des médicaments dans un rayon. En utilisant des représentations visuelles de rectangles inscrits, il peut déterminer comment maximiser l’espace tout en conservant l’accessibilité des produits. Cette approche visuelle, que ce soit pour l’éducation ou pour des usages pratiques, est essentielle pour toute personne désireuse de comprendre l’importance et l’application du rectangle inscrit en géométrie.

Applications Pratiques Du Rectangle Inscrit Dans La Vie

Le rectangle inscrit joue un rôle essentiel dans divers domaines de la vie quotidienne, que ce soit en architecture, en design ou en ingénierie. Par exemple, en architecture, le concept de rectangle inscrit permet de maximiser l’espace tout en préservant l’esthétique. Lors de la conception de bâtiments, les architectes utilisent souvent cette approche pour déterminer la surface optimale à construire tout en répondant aux exigences fonctionnelles. Cela démontre comment les principes mathématiques s’appliquent directement à la création d’espaces habitables et fonctionnels.

Dans le domaine du design graphique, les designers utilisent des rectangles inscrits pour créer des mises en page équilibrées et harmonieuses. L’utilisation des grands rectangles pour séparer les sections d’une page permet une meilleure lisibilité et un attrait visuel plus fort. En jouant avec les dimensions du rectangle inscrit, les designers peuvent optimally utilize chaque partie de la page, assurant que l’information est présenté clairement et efficacement.

Un autre aspect intéressant concerne l’industrie automobile. Les ingénieurs utilisent le concept de rectangle inscrit pour optimiser l’aérodynamisme des véhicules, ce qui peut améliorer leurs performances. En formant des structures qui respectent les proportions définies par le rectangle inscrit, les concepteurs cherchent à réduire la résistance à l’air. Cela démontre l’importance du principe dans des innovations technologiques qui influencent notre quotidien.

Enfin, en mathématiques, le rectangle inscrit est souvent utilisé dans des problèmes d’optimisation. Par exemple, les étudiants sont fréquemment confrontés à des exercices sur la manière de “trouver la área do maior retangulo que pode ser inscrito” dans un cercle, ce qui non seulement fixe une compréhension théorique, mais agit également comme un pont vers des applications concrètes dans la vie de tous les jours.

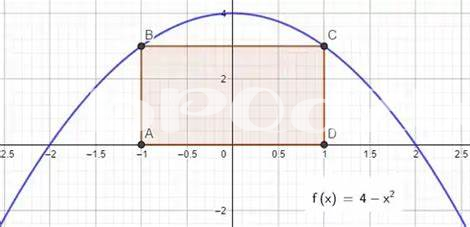
Erreurs Courantes À Éviter Dans Les Démonstrations

Lors de la démonstration d’un rectangle inscrit, certaines erreurs peuvent souvent survenir, entraînant confusion et malentendus. Tout d’abord, il est crucial de ne pas confondre la position et les dimensions du rectangle par rapport au cercle. Un rectangle inscrit est déterminé par les points d’intersection avec le cercle, et négliger cette méthode peut conduire à des affirmations incorrectes sur la superficie maximale, ou pour certains, à l’encontre a area do maior retangulo que pode ser inscrito. Une autre confusion fréquente réside dans l’absence d’une visualisation adéquate, rendant difficile la compréhension des relations géométriques fondamentales.

En outre, certains pourraient omettre de préciser les conditions nécessaires à l’existence d’un rectangle inscrit. Par exemple, supposons qu’un étudiant essaye de démontrer des propriétés sans s’assurer que le cercle abrite le rectangle dans ses dimensions appropriées. Cela pourrait aboutir à des erreurs de calcul et une interprétation erronée des concepts. De plus, il est essentiel de rappeler que les démonstrations doivent être accompagnées d’une logique rigoureuse et de justifications claires. Un manque d’explications claires pourrait faire d’un argument potentiellement solide une simple affirmation, ce qui n’aide pas à la compréhension approfondie des propriétés fascinantes des rectangles inscrits.

Erreur Courante	Description
Confusion sur la position	Ne pas respecter les points d’intersection avec le cercle.
Visualisation inadéquate	Absence de schémas clairs pour représenter les relations.
Omissions de conditions	Ne pas établir les bases des démonstrations correctement.

Zoom Sur Des Exemples Célèbres De Rectangles Inscrits

Les rectangles inscrits se retrouvent dans de nombreux contextes célèbres, prouvant ainsi leur pertinence en géométrie. Prenons l’exemple du fameux Minitel, utilisé par de nombreux Français dans les années 80. La conception de cet outil reposait sur des formes rectangulaires, illustrant comment ces figures géométriques peuvent influencer des technologies de communication modernes. Un rectangle, s’inscrivant dans un cadre, illustre parfaitement l’idée que l’information peut être contenue et organisée de façon efficace.

Un autre exemple marquant se situe dans le monde de l’architecture, où des bâtiments emblématiques utilisent le principe du rectangle inscrit pour optimiser l’espace. Par exemple, le palais de Versailles présente de nombreuses salles dont les dimensions répondent à ce concept. Cette approche notammant s’inspire des calculs de proportionnalité, ce qui rend les espaces non seulement esthétiques mais également fonctionnels. En observant ces structures historiques, on peut comprendre la beauté et l’harmonie qui peuvent être atteintes grâce à des principes géométriques simples.

Enfin, le travail de grands mathématiciens comme Euclide a été fondamental dans l’étude des rectangles inscrits. Leurs théories ont ouvert la voie à des calculs plus complexes et à l’exploration d’autres figures. Ces modèles ont été transmis à travers le temps, créant une base solide pour notre compréhension contemporaine des géométries. Leurs apports sont incontestablement le fondement sur lequel repose notre connaissance des propriétés des rectangles inscrits et de leur impact dans divers domaines.